Jälkijännitetyn palkin leikkauskestävyys

Betoni ja esijännitetyt rakenteet

Betonin alhaisen vetolujuuden, mutta korkean puristuslujuuden vuoksi betoni soveltuu hyvin esijännitettäväksi. Esijännittäminen parantaa betonin ominaisuuksia myös leikkauskestävyyden näkökulmasta. Erityisesti jälkijännittäminen parantaa leikkauskestävyyttä, sillä jälkijännittäminen mahdollistaa kaarevan jännegeometrian, jolloin puristusjännitystä voidaan suoraan jännekulkuun verrattuna muodostaa enemmän päävetojännitysten suuntaisesti. Diplomityössä tutkittiin jälkijännitetyn palkin leikkauskestävyyttä. Tavoitteena oli selkeyttää vastikään julkaistun toisen sukupolven betonieurokoodin käyttöä jälkijännitetyn palkin leikkausmitoituksessa sekä verrata laskentamenetelmiä ja tuloksia nykyisin käytössä oleviin suunnitteluohjeisiin, ensimmäisen sukupolven betonieurokoodiin sekä sen soveltamisohjeeseen NCCI2:seen.

Taustaa:

Palkkien leikkauskestävyyden määritys on yksi monimutkaisimmista, mutta olennaisimmista aiheista teräsbetonipalkkien suunnittelussa. Ilmiön tutkimiseen saatavilla oleva data on perinteisesti koostunut yksiaukkoisten palkkien koekuormitusaineistosta ja usein on tarkasteltu ainoastaan palkin taipumaa ja kuorman suuruutta. Aineistosta saatujen havaintojen perusteella suunnitteluohjeiden laskentakaavat ovat kalibroitu, monesti empiirisin menetelmin laajoihin tietokantoihin perustuen. Myös mekaanisia malleja on ehdotettu rationaaliseksi lähestymistavaksi leikkausmitoitukseen. Erilaisten mittaustekniikoiden, kuten digitaalisen kuvakorrelaation kehittyminen on mahdollistanut erilaisten leikkausmitoituksen mekaanisten mallien ja niissä esiintyvien leikkausrasitusten siirtymismekanismien tarkemman tutkimisen.

Suomessa leikkauskestävyyden mitoitus tehdään tällä hetkellä ensimmäisen sukupolven betonirakenteiden eurokoodin [4] mukaisesti. Poikkeuksena tähän ovat taitorakenteet, joissa noudatetaan ensisijaisesti eurokoodin betonirakenteiden soveltamisohjetta NCCI 2 [2]. Toisen sukupolven betonieurokoodi [5] on julkaistu, mutta kansallisia liitteitä ei ole vielä julkaistu, eikä standardia ole vielä otettu suunnittelutyössä käyttöön. Jälkijännitetyn palkin leikkausmitoituksessa on muuttunut erityisesti leikkausraudoittamattoman palkin mitoitus, joka toisen sukupolven betonieurokoodissa perustuu uuteen mitoitusteoriaan (critical shear crack theory). Uusi mitoitusteoria perustuu mekaaniseen malliin, kun aiemmin leikkausraudoittamattoman palkin leikkausmitoitus on perustunut empiiriseen malliin. Myös leikkausraudoitetun palkin leikkauskestävyyden laskentakaavoja on päivitetty, mutta mitoitus perustuu edelleen muuttuvakulmaiseen ristikkomalliin, joten muutokset eivät ole yhtä merkittäviä kuin leikkausraudoittamattoman palkin tapauksessa.

Teräsbetonirakenteen leikkauskestävyyttä tarkastellaan yleensä murtotilanteessa, jolloin poikkileikkaus oletetaan halkeilleeksi. Leikkausrasitukset välittyvät halkeilleessa betonirakenteessa monin eri tavoin: Halkeilemattoman betonin puristusvyöhykkeen välityksellä, runkoaineksen lukkiutumisesta, pääraudoituksen vaarnavaikutuksella, leikkausraudoituksella ja betonin jäännösvetolujuuden avulla. Leikkausmitoitusmallista riippuen joidenkin välittymismekanismien vaikutuksia ei välttämättä oteta huomioon.

Teräsbetonirakenteella leikkauskestävyyden laskennassa käytetään eri laskentamallia riippuen siitä, onko rakenne leikkausraudoitettu vai leikkausraudoittamaton. Teräsbetonipalkeilla leikkausraudoittamattomaksi käsitetään rakenne, johon on sijoitettu vähimmäisleikkausraudoitus. Vastaavasti leikkausraudoitetussa rakenteessa leikkausraudoituksen määrä on tätä suurempi. Leikkausraudoitetussa rakenteessa leikkausmurron otaksutaan tapahtuvan leikkausraudoituksen venymän,
betonin kaltevan puristuskentän murtumisen tai näiden yhteisvaikutuksen seurauksena. Tällöin halkeilu on jakaantunutta ja rakenteella on muodonmuutoskykyä. Leikkausraudoittamattomissa rakenteissa sen sijaan leikkausmurron otaksutaan tapahtuvan, kun venymä keskittyy paikallisesti kriittiseen leikkaushalkeamaan, jolloin muodonmuutoskyky on hyvin rajallinen.

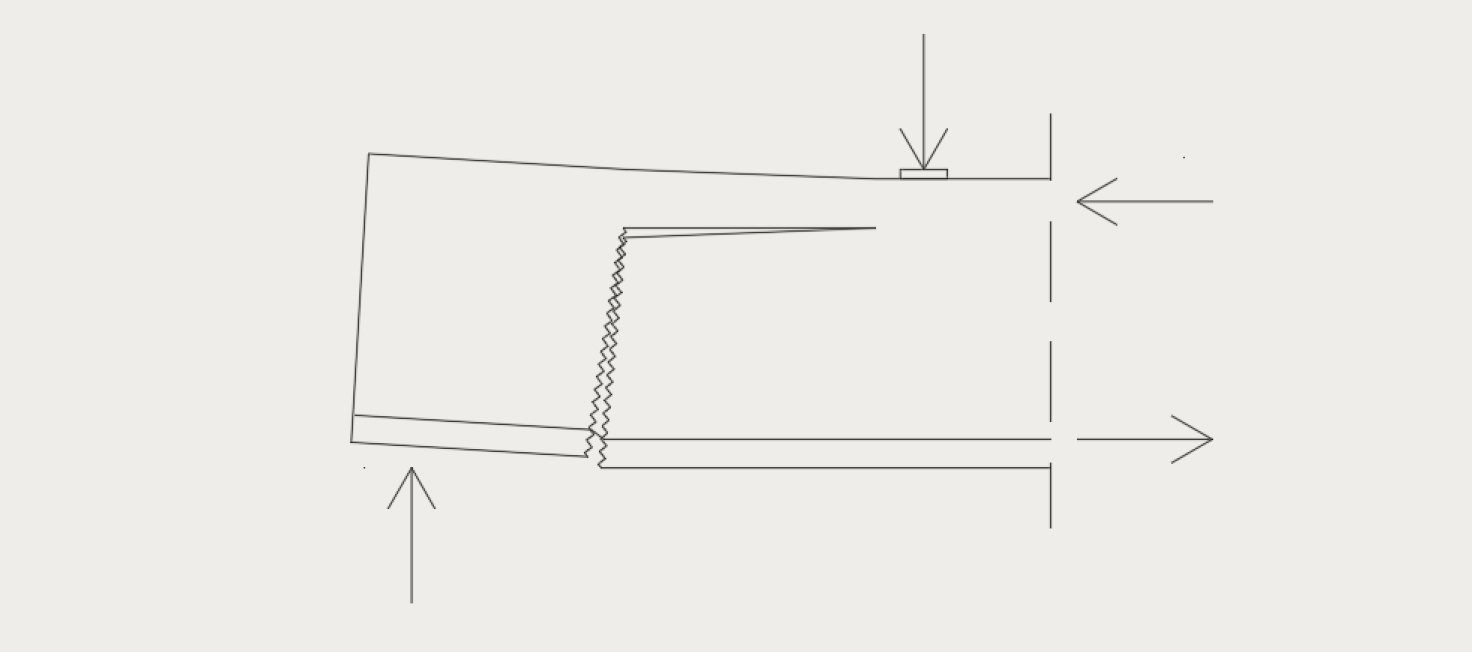
Toisen sukupolven betonieurokoodin leikkausraudoittamattoman palkin mitoitusmenettely perustuu ”Critical Shear Crack” -teoriaan. Teorian pääotaksuma on, että leikkauskestävyyden määrittää kriittisen leikkaushalkeaman kehittyminen, joka häiritsee leikkausrasitusten välittymistä betonissa. Leikkauskestävyys näin ollen riippuu kriittisen leikkaushalkeaman avaumasta ja karheudesta sekä betonin puristuslujuudesta. Mitä suurempi halkeaman avauma on, sitä pienempi on rakenneosan leikkauskestävyys. Tyypillisesti halkeama alkaa kehittyä vetoalueelta taivutushalkeamasta. Palkin kuormitustason edelleen kasvaessa, halkeama alkaa kehittyä palkin pituussuuntaan, jolloin pystysuuntaisen halkeaman eri pinnat liukuvat toisiinsa nähden kuvan 1 mukaisesti. Teorian mekaanisen mallin perusolettama on, että kriittisen leikkaushalkeaman leveys w on suoraan verrannollinen kontrollisyvyyden pituussuuntaisen muodonmuutoksen εref ja rakenneosan tehollisen korkeuden d tuloon kaavan (1) mukaisesti.

Tämän olettaman pohjalta on muodostettu yksinkertainen analyyttinen muoto murtokriteerille, joka voidaan esittää hyperbolisena funktiona kaavan (2) mukaan.

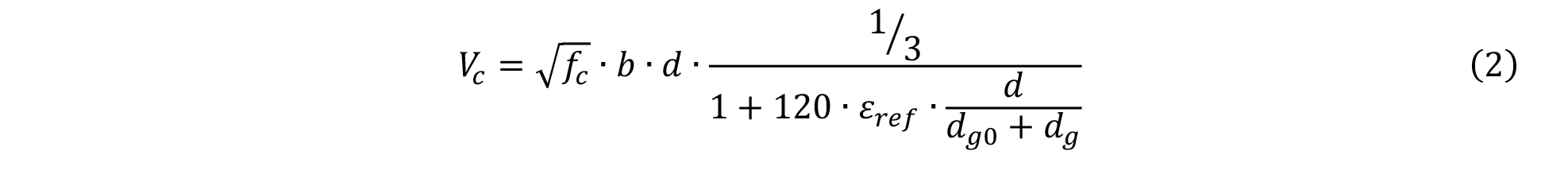
jossa
f_c = betonin puristuslujuus
b = rakenneosan leveys
d_go = betonin runkoaineskoon vertailuarvo (16 mm)
d_g = runkoaineskoon enimmäisarvo

Parametri _εref tarkoittaa pituussuuntaista muodonmuutosta etäisyydellä 0,6 · d puristetusta pinnasta, joka on johdettu poikkileikkausanalyysistä olettaen lineaarielastinen materiaalimalli ja jättäen betonin vetolujuuskapasiteetti huomioimatta. Toisen sukupolven betonirakenteiden eurokoodiin laskentakaava on vielä kalibroitu ja johdettu edelleen helpommin käytettävään muotoon, jolloin poikkileikkaussuureiden sekä poikkileikkauksessa vaikuttavien voimasuureiden avulla voidaan määrittää leikkauskestävyys kaavan (3) mukaan.

jossa
γV = leikkausmitoituksen osavarmuuskerroin
ρl = raudoitussuhde
d_dg = kokovaikutus, joka kuvaa halkeaman ja murtopinnan karheutta, huomioiden betonityypin ja sen runkoaineksen ominaisuudet
kvp = aksiaalisen voiman huomioon ottava kerroin
a_v = mekaaninen leikkausjänne

Kaavan sulkulausekkeen sisällä oleva osa sisältää kaksi teräsbetonisen palkin leikkauskestävyyteen merkittävästi vaikuttavaa tekijää: Leikkausjänteen vaikutuksen ja kokovaikutuksen.

Leikkausjänteen arvo riippuu palkin kuormitusasennosta. Yleistäen esimerkiksi pistekuormalla kuormitetulla yksiaukkoisella palkilla leikkausjänteen suuruus on sama kuin kuorman etäisyys tuelta. Kun kuorma on lähellä tukea, taivutushalkeamat eivät ulotu betonin sisäiseen kaltevaan puristussauvaan, jolloin vetoraudoitus myötää ja täysi plastinen kestävyys saavutetaan. Kun kuormaa viedään pidemmälle tuelta betonin sisäisen kalteva puristussauva alkaa taittua taivutushalkeilun ulottuessa yhä enemmän puristusvyöhykkeelle. Tällöin vetoraudoitus ei myötää ja plastinen kestävyys yliarvioi palkin kestävyyden. Edelleen kuorman siirtyessä kauemmas tuelta vetoraudoitus myötää jälleen ja plastinen kestävyys saavutetaan. Yleistäen voidaan siis sanoa, että hyvin pienellä tai riittävän suurella leikkausjänteellä saavutetaan täysi leikkauskapasiteetti. Tässä työssä ei tarkastella tilannetta, jossa leikkausjänne on hyvin pieni.

Kokovaikutus tarkoittaa sitä, kun teräsbetonirakenteen tehollisen korkeuden kasvaessa myös kaltevan halkeaman leveys kasvaa, jolloin runkoaineksen lukkiutumisen avulla halkeaman yli välittyy vähemmän leikkausrasitusta eli rakenneosan normalisoitu leikkauskestävyys pienenee. Kokovaikutus on riippuvainen myös raudoitussuhteesta sekä leikkausjänteestä, johon vaikuttaa rakenneosan aksiaalinen voima. Kokovaikutus ei ole yhtä merkittävä leikkausraudoitetulla rakenteella, sillä raudoitus estää halkeamien avautumista. Toisin sanoen leikkausraudoitus sitoo halkeamapintoja yhteen, jolloin runkoaineksen lukkiuma säilyy leikkausraudoitetulla rakenteella paremmin verrattuna leikkausraudoittamattomaan rakenteeseen.

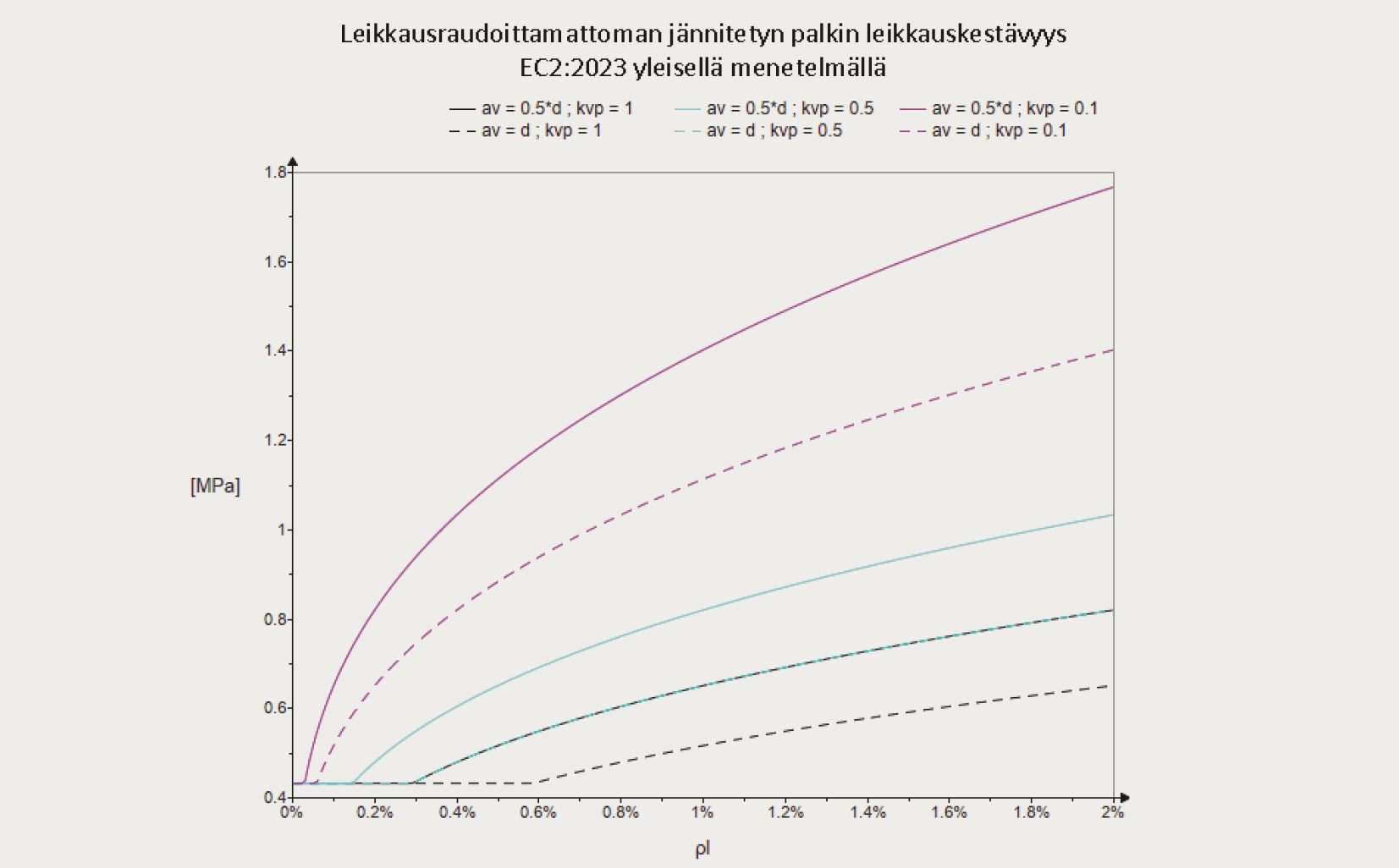
Kuvassa (2) on esitetty toisen sukupolven eurokoodin mukaisia leikkausraudoittamattoman aksiaalisesti puristetun palkin leikkauskestävyyden tuloksia raudoitussuhteen funktiona, varioiden mekaanista leikkausjännettä av sekä aksiaalisen voiman huomioon ottava kerrointa kvp. Mekaaninen leikkausjänne voi saada arvoja välillä ja aksiaalisen voiman huomioon ottava kerroin 0,1…1,0. Mitä pienemmät arvot ovat, sitä suurempi leikkauskestävyys saavutetaan, mikä voidaan nähdä myös kuvaajasta.

Tutkimusasetelmat:

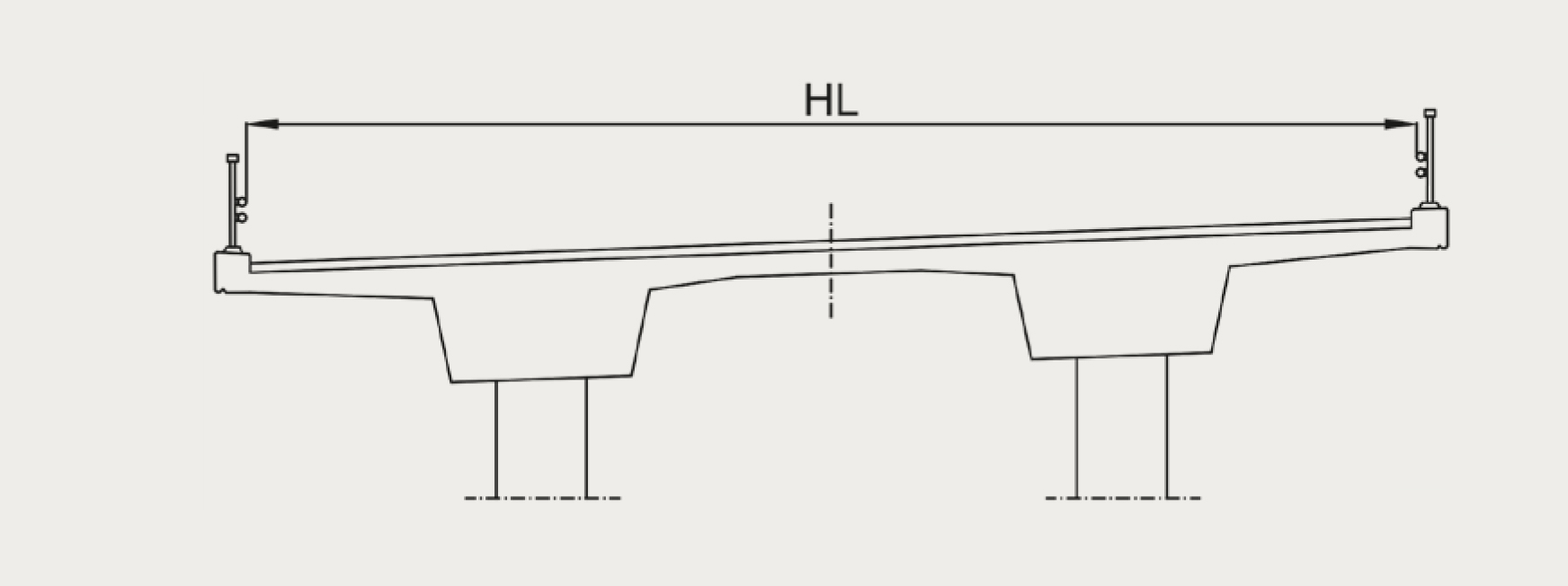
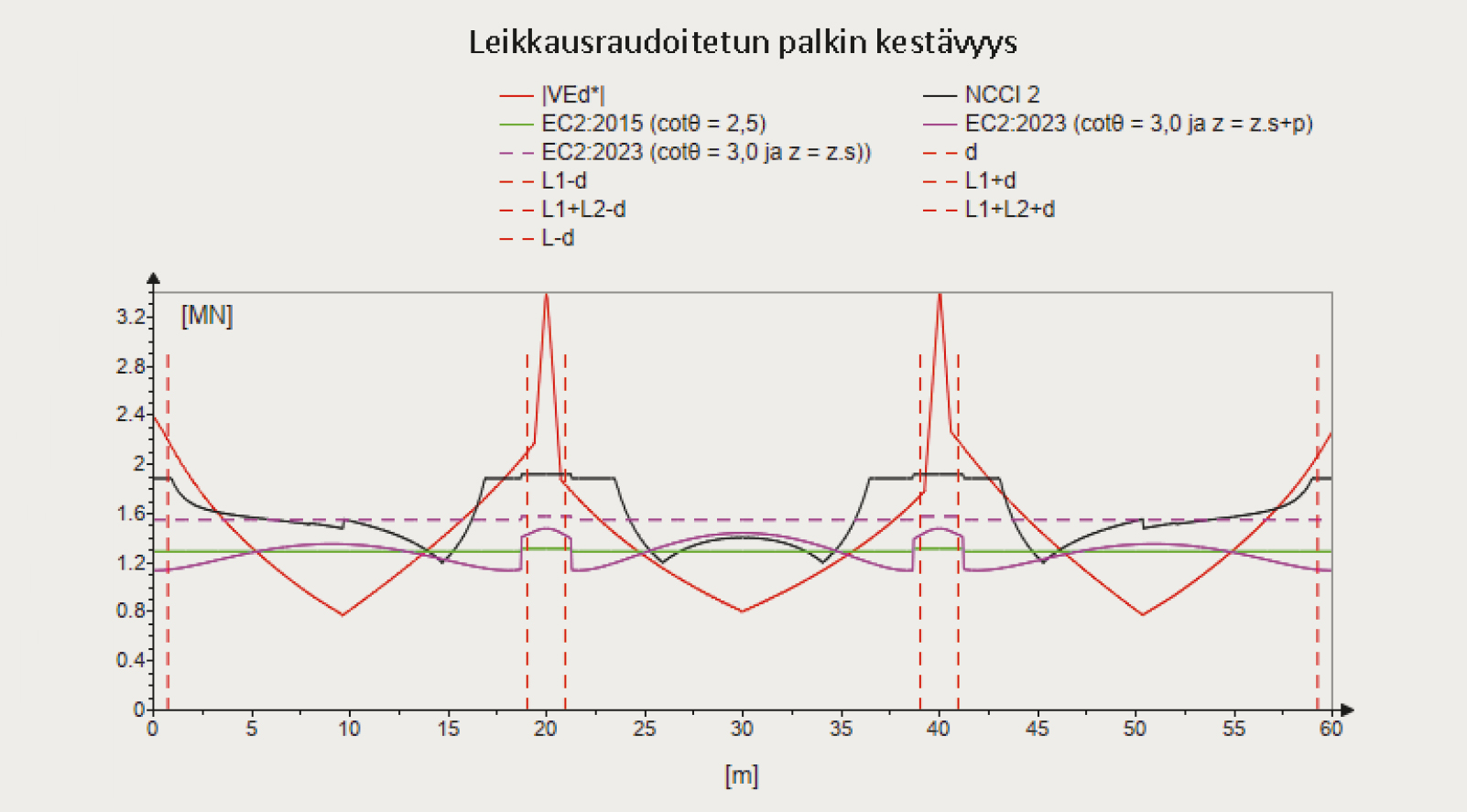
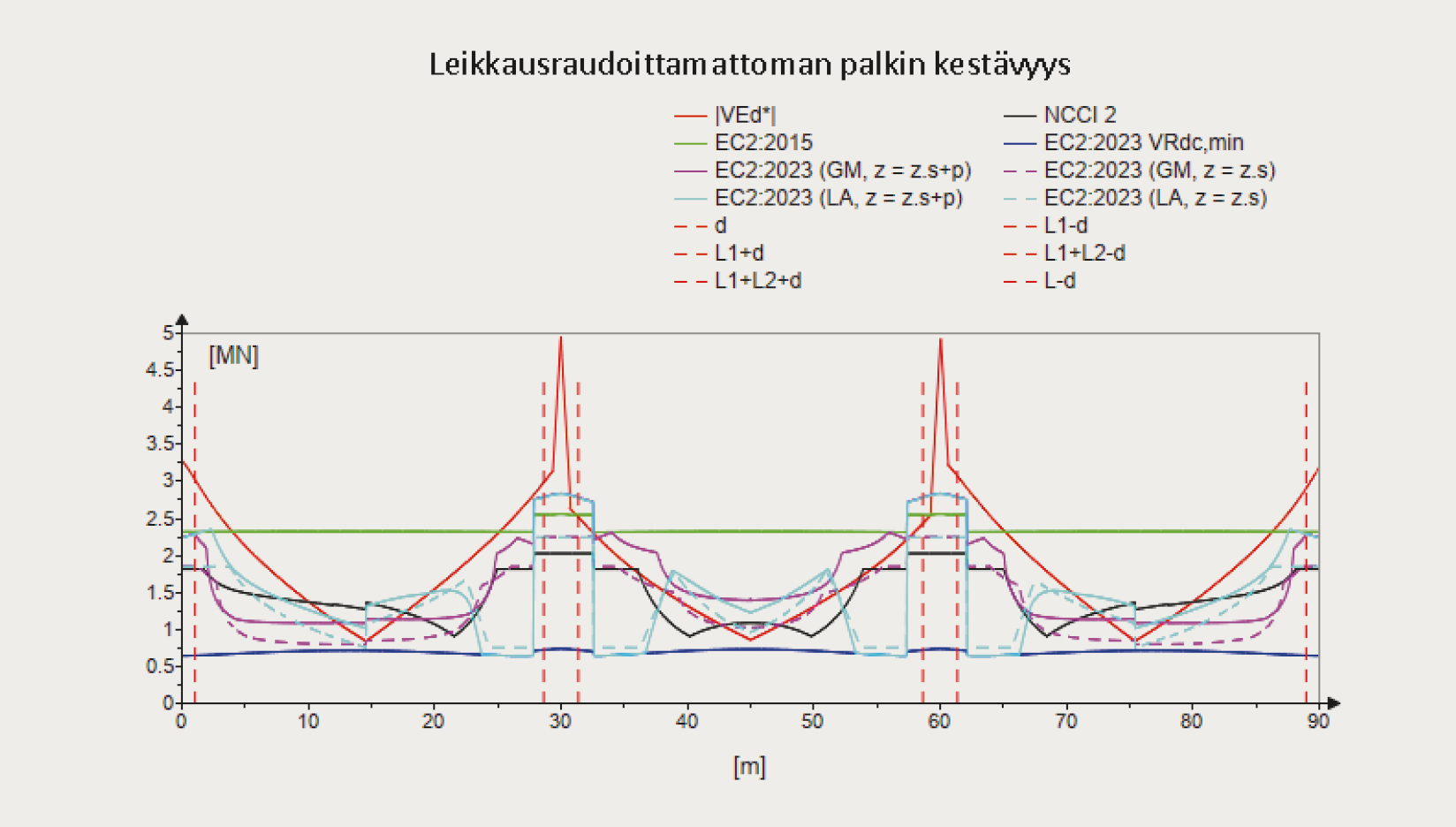
Tutkimus koostuu teoriaosuudesta sekä laskentatarkasteluista. Laskentatarkasteluissa tarkasteltiin jälkijännitettyjen palkkien leikkauskestävyyttä sekä leikkausrasituksesta aiheutuvaa lisävetovoimaa 12:lla eri jälkijännitettyä kaksipalkkista palkkisiltaa (kuva 3) jäljittelevällä palkkimallilla. Laskentatapauksista 6 on kaksiaukkoisia ja 6 kolmiaukkoisia palkkeja. Palkkeihin vaikuttivat NCCI 1 [1] mukaiset tieliikenteen siltojen kuormat. Malleja analysoitiin koko palkin pituudelta ja tuloksia vertailtiin suunnitteluohjeiden betonirakenteiden eurokoodin ensimmäisen ja toisen sukupolven sekä soveltamisohjeen NCCI 2 välillä (kuvat 4 ja 5). Kriittisissä poikkileikkauksissa, eli tehollisen korkeuden päässä tuilta, laskentatulokset taulukoitiin numeroarvoina. Lisäksi tehtiin yksittäisiä laskentatarkasteluja, joissa tutkittiin eri yksittäisten tekijöiden vaikutusta jälkijännitettyjen palkkien leikkauskestävyyteen. Yksittäisissä laskentatarkasteluissa laskentatapaukset valikoitiin edellä mainituista 12 laskentatapauksesta, mutta jännevoima sekä jännityshäviöt määritettiin tarkasti.

Teräsbetonirakenteen toiminta leikkausrasituksessa voidaan jakaa kolmeen alakohtaan:

1. Halkeilemattoman betonirakenteen toiminta
2. Halkeilleen leikkausraudoittamattoman betonirakenteen toiminta
3. Halkeilleen leikkausraudoitetun betonirakenteen toiminta

Näistä kohdan 1. rakenteiden oletetaan toimivan homogeenisen rakenteen tavoin ja mitoitus tehdään pääjännityksiä tarkastelemalla. Työssä tarkasteltiin rakenteita vain kohtien 2. ja 3. mukaisesti, sillä toisen sukupolven betonieurokoodin mitoitusmallit otaksuvat halkeilleen poikkileikkauksen. Tutkimuksessa leikkausraudoittamattomalla palkilla tarkoitetaan siis palkkia, johon on sijoitettu vähimmäisleikkausraudoitus. Täysin raudoittamattomat matalat palkit rajattiin tutkimuksen ulkopuolelle. Laskentatarkasteluissa leikkausraudoitettuihin palkkeihin oli sijoitettu ainoastaan eurokoodin mukainen vähimmäisleikkausraudoitus.

Tutkimuksen tavoitteena oli selkeyttää toisen sukupolven betonirakenteiden eurokoodin käyttöä leikkausmitoituksessa sekä löytää hyviä käytäntöjä jälkijännitettyjen palkkien suunnitteluun toisen sukupolven eurokoodin mukaisesti. Leikkausraudoittamattoman sekä leikkausraudoitetun rakenteen mitoitukseen ja lisävetovoiman määritykseen pyrittiin löytämään suunnittelun kannalta käytännöllisiä ratkaisuja. Laskentatarkastelujen tavoitteena oli vertailla eroja leikkauskestävyydessä ensimmäisen ja toisen sukupolven betonieurokoodin sekä eurokoodin soveltamisohjeen NCCI 2 välillä, sekä selvittää eri laskentatapauksilla eroja leikkauskestävyydessä leikkausraudoitettuna minimileikkausraudoituksella ja leikkausraudoittamattomana eurokoodin toisen sukupolven eurokoodin mukaisesti.

Toisen sukupolven betonirakenteiden eurokoodissa rakenteen leikkauskestävyys määritetään käyttäen jännityksiä. Tällöin leikkauskestävyyden suuruusluokan arviointi on helpompaa poikkileikkauksesta riippumatta, verraten leikkauskestävyyden tarkasteluun voimana. Työssä kuitenkin leikkauskestävyyttä tarkasteltiin voimana, jolloin vertailu eri suunnitteluohjeiden laskentakaavoihin sekä laskentatuloksiin oli helpompaa.

Laskentatulosten tarkastelu:

Leikkausmitoituksessa palkin sisäinen momenttivarsi z lasketaan yksinkertaistettuna kaavalla, jossa d on tehollinen korkeus. Toisen sukupolven eurokoodin mukaisessa leikkauskestävyyden laskennassa tulee lähtökohtaisesti käyttää jänneraudoituksen ja tavanomaisen vetoraudoituksen poikkileikkausalalla painotettua tehollista korkeutta (kaava 4), ellei pelkkä tavanomainen raudoitus pysty vastaanottamaan poikkileikkauksessa vaikuttavaa vetovoimaa. Tehollisen korkeuden lisäksi jänneraudoite huomioidaan vastaavasti myös raudoitussuhteen laskennassa (kaava 5).

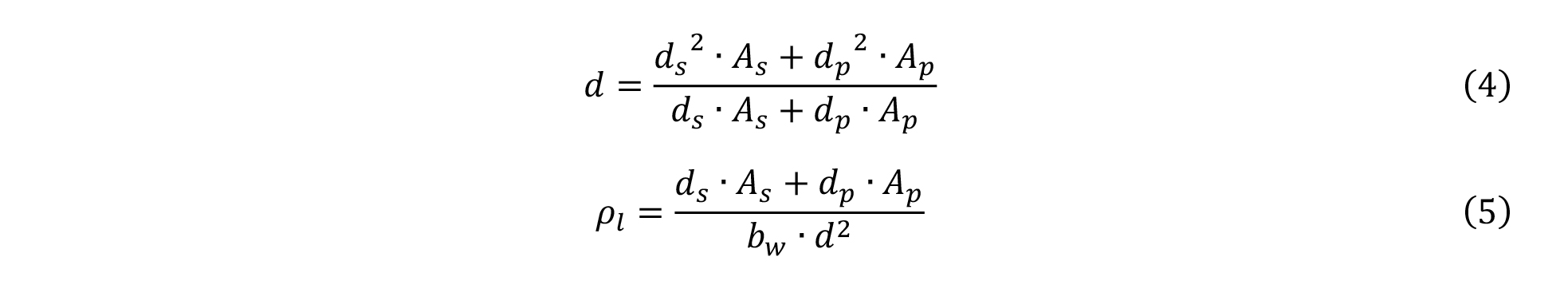
jossa
d_s = tavanomaisen raudoituksen tehollinen korkeus
d_p = jänneraudoituksen tehollinen korkeus
A_s = tavanomaisen raudoituksen poikkileikkausala
A_p = jänneraudoituksen poikkileikkausala

Laskentatuloksista havaittiin, että toisen sukupolven eurokoodin mukainen leikkausraudoittamattoman jälkijännitetyn palkin leikkauskestävyys oli parempi, kun palkin teholliselle korkeudelle ja raudoitussuhteelle käytettiin jänneraudoitteen poikkileikkausalan huomioivia arvoja. Vaikka jänneraudoite yleisesti on tavanomaisen vetoraudoituksen sisäpuolella poikkileikkauksessa ja näin ollen vähentää tehollisen korkeuden arvoa, joka johtaa leikkauskestävyyden vähenemiseen, niin toisaalta jänneraudoite nostaa merkittävästi raudoitussuhdetta, joka puolestaan parantaa leikkauskestävyyttä. Kokonaisvaikutukseltaan jänneraudoituksella havaittiin olevan leikkauskestävyyttä lisäävä vaikutus. Tämä todennettiin vielä tarkastelemalla yhtä laskentatapausta varioimalla pääraudoitussuhdetta välillä 0,4 %…2,0 %. Havainnon todettiin helpottavan leikkausraudoittamattoman rakenteen mitoitusta, sillä ei erikseen tarvitse tarkastella pystyykö tavanomainen vetoraudoitus vastaanottamaan poikkileikkauksessa vaikuttavan vetovoiman, vaan jänneraudoite voidaan ottaa aina laskennassa huomioon, kun määritetään leikkausmitoituksessa käytettävää sisäistä momenttivartta ja raudoitussuhdetta.

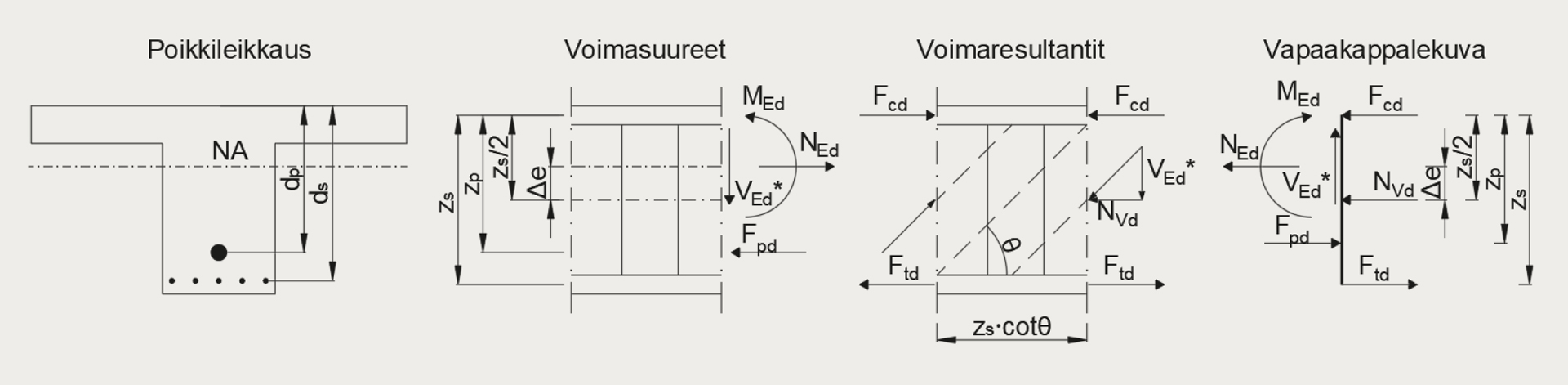
Leikkausraudoitettuna mitoitetulla jälkijännitetyllä palkilla sen sijaan ns. painotetun tehollisen korkeuden mukaan laskettu leikkauskestävyyden arvo on luonnollisesti pienempi kuin käytettäessä pelkän tavanomaisen vetoraudoituksen tehollista korkeutta, mikäli jänneraudoite sijaitsee tavanomaisen raudoitteen sisäpuolella poikkileikkauksessa. Tutkimuksessa kuitenkin todettiin, että mikäli leikkausrasituksesta aiheutuva lisävetovoima otetaan laskennassa huomioon leikkausmitoitusmallin mukaisesti (kuva 6), voidaan leikkausraudoitetun palkin leikkausmitoituksessa käyttää aina tavanomaisen vetoraudoituksen mukaista tehollisen korkeuden arvoa.

Toisen sukupolven betonieurokoodissa leikkausraudoitetun palkin leikkausmitoitusmallin puristuskentän kulma voidaan valita tavanomaisilla betonirakenteilla väliltä n. 21,8…45°. Poikkileikkauksen ollessa puristettu keskimäärin vähintään 3 MPa, voidaan puristuskentän kulmaksi valita loivimmillaan n. 18,4°. Laskentatarkasteluissa käytettiin loivinta mahdollista kulmaa, jolloin saavutettiin suurin mahdollinen leikkauskestävyys. Useimpien laskentatapausten leikkauskestävyys oli suurempi leikkausraudoitettuna minimileikkausraudoituksella kuin leikkausraudoittamattomana toisen sukupolven eurokoodin mukaan laskettaessa.

Huomioitavaa kuitenkin on, että työssä ei tarkasteltu käyttörajatilan ilmiöitä, kuten uuman halkeilua. Loivan puristuskentän kulman käyttö vaatii suurempia venymiä leikkausraudoitukselta ja vähentää kaltevan puristuskentän kestävyyttä sekä näin ollen aiheuttaa uuman halkeilua. Ilmiötä olisi mahdollista tarkastella toisen sukupolven betonieurokoodin liitteen G mukaisesti tasomuodonmuutostilan avulla.

Laskentatulosten vertailussa ensimmäisen ja toisen sukupolven eurokoodin ja NCCI 2 välillä havaittiin, että suurin leikkauskestävyys leikkausraudoittamattomana saavutettiin toisen sukupolven eurokoodin laskentamenetelmillä. Leikkausraudoitetulla palkilla laskenta on lähes vastaava eri eurokoodiversioiden kesken, joten ero niiden välillä johtui ainoastaan toisen sukupolven eurokoodin sallimasta loivemmasta puristuskentän kulmasta. Kuitenkin NCCI 2 mukaan laskettu minimileikkausraudoituksella leikkausraudoitetun palkin leikkauskestävyys oli suurempi kuin kummankaan eurokoodiversion mukaan laskettu. NCCI 2 mukaista parempaa leikkauskestävyyttä selittää se, että NCCI 2 mukaisessa laskentatavassa leikkausraudoitetulla rakenteella leikkauskestävyydessä voidaan huomioida myös betonin osuus, jota lisäksi voidaan korottaa palkin ollessa puristettu.

Jälkijännitetyn palkin leikkauskestävyyteen vaikuttavat tekijät:

Kaarevalla jännegeometrialla jännevoima yleensä aiheuttaa leikkausvoimaa nähden vastakkaissuuntaisen komponentin, joka luonnollisesti vähentää betonirakenteeseen kohdistuvaa leikkausrasitusta sekä leikkausraudoittamattomalla, että leikkausraudoitetulla palkilla. Leikkausraudoitettuna mitoitetulla jälkijännitetyllä palkilla leikkauskestävyyteen vaikuttavat tekijät voidaan helposti määrittää ja niiden vaikutukset leikkauskestävyyteen ovat selkeitä. Näitä tekijöitä ovat leikkausraudoitussuhde, puristuskentän kaltevuus sekä leikkauspaneelin poikkileikkauksen pinta-ala, mikä riippuu sisäisen momenttivarren korkeudesta sekä leikkaukselle toimivan poikkileikkauksen leveydestä. Lisäksi poikkileikkauksen ollessa puristettu, voidaan puristuskentän kulmaa loiventaa, mutta vaikutus kestävyyteen on enintään 20 % suurempi tavanomaiseen teräsbetonipalkkiin verrattuna.

Leikkausraudoittamattomalla palkilla esijännityksen vaikutus leikkauskestävyyteen on suurempi. Leikkausraudoittamattomalla palkilla leikkauskestävyyteen vaikuttaa merkittävästi kokovaikutus, leikkausjänne, jännegeometria ja aksiaalinen rasitus sekä raudoitussuhde. Näistä esijännitys vaikuttaa myös leikkausjänteeseen tavallisesti pienentäen sen arvoa, jolloin leikkauskestävyys paranee.

Toisen sukupolven betonieurokoodin erityispiirteet leikkausmitoituksessa:

Toisen sukupolven betonieurokoodin mukaisessa jälkijännitetyn palkin leikkausmitoituksessa havaittiin muutamia erityispiirteitä. Lähtökohtaisesti leikkausmitoituksessa jännevoima otetaan voimasuureissa huomioon. Tämä ei kuitenkaan ole välttämättä selvää eurokoodia käytettäessä, sillä voimasuureiden merkinnät ovat samoja jännevoima huomioituna voimasuureissa tai pelkillä ulkoisilla voimasuureilla. Tämän takia työssä käytettiin eri merkintää voimasuureille, joissa jännevoiman vaikutus on mukana. Myöskään käytettävän uuman leikkauspaneelin korkeuden eli sisäisen momenttivarren korkeuden määritys ei ole laskennassa aina selvää. Tutkimuksessa todettiin, että suurimman leikkauskestävyyden leikkausraudoittamattomana saa käyttäen jänneraudoitteen huomioivaa sisäistä momenttivartta ja leikkausraudoitettuna käyttäen ainoastaan tavanomaisen vetoraudoituksen mukaista sisäistä momenttivartta. Lisäksi laskentakaavat voivat olla vaikeasti tulkittavia jälkijännitetyn rakenteen tapauksessa ja erityisesti mikäli käytetään epäsymmetristä poikkileikkausta. Esimerkiksi leikkausraudoitetun palkin mitoituksessa laskentakaavat esitetään suorakaidepoikkileikkaukselle ja epäsymmetrisen poikkileikkauksen tapauksessa voimasuureet tulee muuttaa niin, kuin ne vaikuttaisivat leikkausmitoituksessa käytettävän sisäisen momenttivarren korkeuden puolivälissä. Jälkijännitetylle palkille lisävetovoiman huomioon ottamista mitoituksessa ei toisen sukupolven eurokoodissa ole yksityiskohtaisesti ohjeistettu.

Yleisesti leikkauskestävyyden tarkastelu voidaan tehdä kahdella tavalla: Joko laskemalla aluksi kapasiteetti ja sen jälkeen vertaamalla sitä vaikuttaviin leikkausrasituksiin tai toisinpäin. Leikkauskapasiteetin laskentaa leikkausraudoittamattomana ennen voimasuureiden laskemista siltarakenteissa ei voida tehdä tarkasti, sillä leikkausjännettä ei tiedetä ennen voimasuureiden laskentaa, johtuen liikkuvasta kuormasta. Mikäli esijännitysvoima, poikkileikkaus ja rakenteen kuormitusasento on tiedossa, on myös leikkauskapasiteetti leikkausraudoittamattomana mahdollista määrittää ilman iteraatiota. Tämän vuoksi siltarakenteilla leikkausmitoitus leikkausraudoittamattomana on suositeltavaa tehdä vasta voimasuureiden määrityksen jälkeen. Leikkauskapasiteetin määritys puolestaan leikkausraudoitetulla palkilla voidaan tehdä, sillä voimasuureiden ei tarvitse olla tiedossa leikkauskestävyyden määritystä varten.

Yhteenveto:

Työssä tutkittiin jälkijännitetyn palkin leikkauskestävyyttä kirjallisuusselvityksenä, että laskennallisin tarkasteluin. Teoriaosassa koottiin yhteen tämänhetkinen teoria jälkijännitettyjen palkkien leikkauskestävyydestä. Laskentatarkasteluissa keskityttiin erityisesti toisen sukupolven betonieurokoodin mukaiseen laskentaan ja vertailulaskentaa tehtiin myös ensimmäisen sukupolven betonieurokoodin sekä eurokoodin soveltamisohjeen NCCI 2 mukaan.

Laskentatuloksia tarkasteltiin 12 eri jälkijännitettyä palkkisiltaa jäljittelevällä palkkiallilla ja tulokset analysoitiin verraten muihin laskentamenetelmiin. Tulokseksi saatiin esimerkinomaiset prosessikaaviot toisen sukupolven betonieurokoodin mukaisesta leikkausmitoituksesta sekä leikkausraudoitettuna, että leikkausraudoittamattomana. Lisäksi avattiin haastavia kohtia toisen sukupolven eurokoodin mitoitusmenettelyssä ja annettiin suosituksia laskentaan. Tuloksia voidaan hyödyntää myöhemmin eurokoodin kansallisen liitteen ja soveltamisohjeen päivitystyössä.